Lexicon
This article describes a few words commonly used in computational geometry and explains their meaning (and how they are used in this documentation). The list is going to be maintained and expanded.
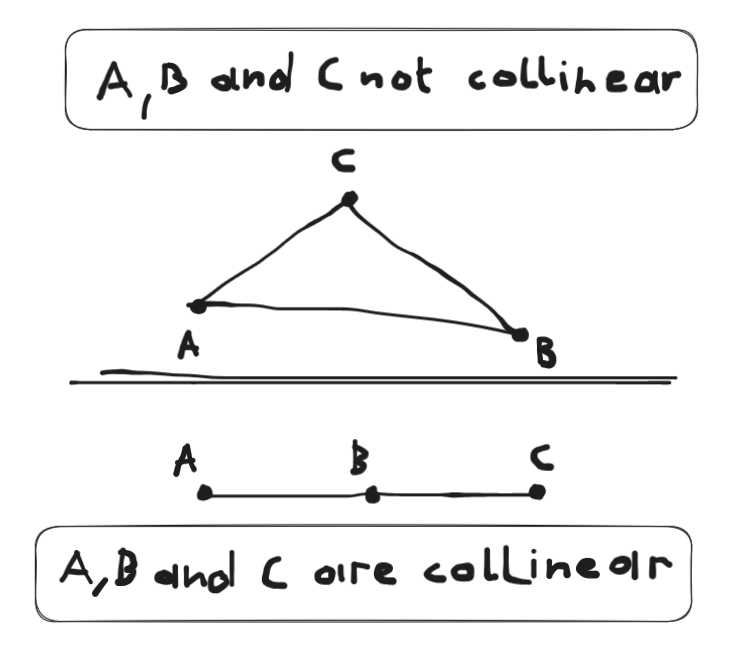
Collinear
Sometimes spelled colinear. Three points are considered to be collinear if a single straight line can be drawn through all of them. Collinear points often lead to problems in algorithms since they do not form a triangle (or a triangle with zero area).
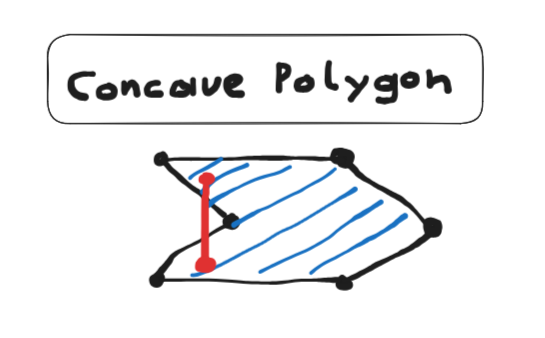
Concave
A boundary is concave if it is not convex. In other words, a boundary, such that not every point inside can be connected to each other point by a simple straight line.
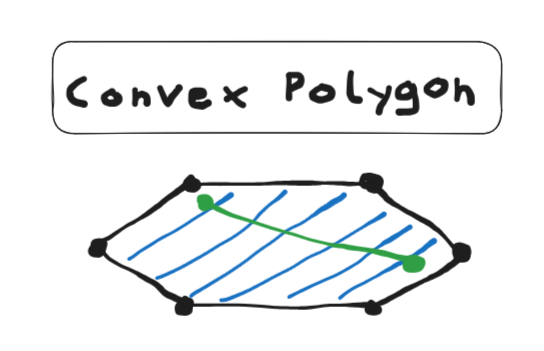
Convex
A boundary (for example a polygon) is convex if from every point inside it, all other points are visible (and you can connect them with a straight line without ever intersecting the boundary)
Degenerate Case
Special cases in geometric algorithms that are encountered during the execution, usually due to ill-formed input (triangles with collinear points, zero-length lines, a circle with infinite radius etc.), precision problems or some form of limit is reached.
Dynamic
In the context of data structures in computational geometry, dynamic data structures and dynamic algorithms react well to the changes in the data. I.e. they are quick to update and do not need a complete reconstruction. Many problems in video game development are dynamic, as GameObjects and Entities move around the world.
Since both types of problems can occur (dynamic for moving object or static for non-moving object), choosing the right structure for the task at hand will improve the performance!
Euclidean Distance
The most common or “regular” way of measuring the distance between two points in space. For 2D, mathematically speaking, it looks like so: 
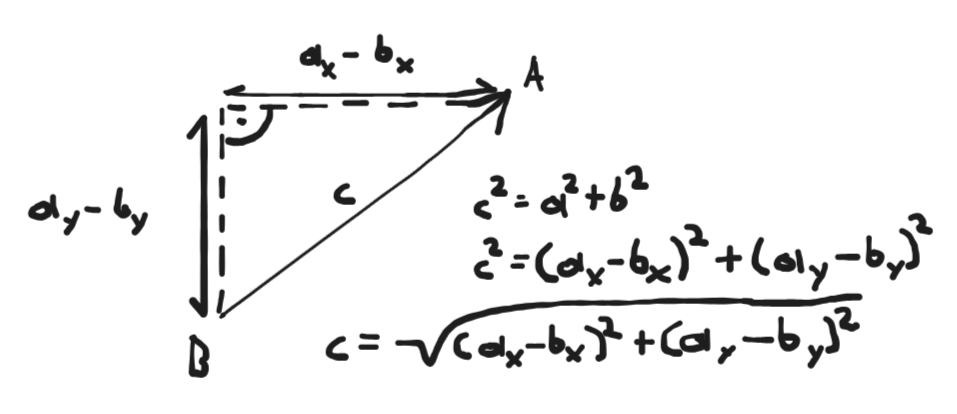
In Unity we do the same with the following code:
Vector2.Distance(a, b);Manhatten Distance
Also called taxicab distance or city block distance. As the name would suggest, it is a measurement of distances within a “grid” i.e. in a space where you can only move along the axes and not along any diagonal.
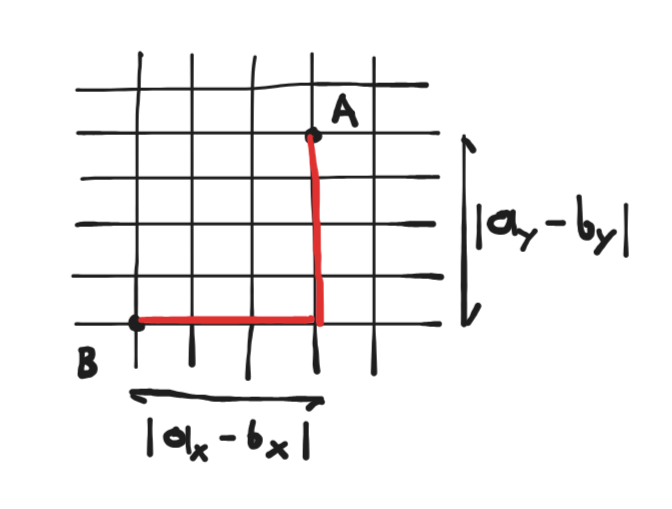
For 2D the distance metric is defined as 
. In Unity we can express the mathematical formula with the following code:
Mathf.Abs(a.x - b.x) + Mathf.Abs(a.y - b.y)Nearest Neighbor Search
Abbreviated NN Search or NNS. A type of query that, given an input position, will return the nearest/closest point or shape that is inside of a spatial data structure. A variant called kNN Search return the k closest points or shapes to a given position.
Spatial Data Structure
A data structure specialized for sorting and finding geometric objects in an d-dimensional space fast. Examples of these are KD-Trees, Quadtrees, etc. The structures can be subtly different to handle for example dynamic or static objects better.
An example for structures that handle geometric objects that are not just points, is the Ball* Tree, that manages a collection of circles or spheres.
Sweep line algorithm
A category of algorithms were a line is “swept” through a geometric data set. It can be done in numerous ways, but usually goes from a “highest” point to a “lowest” point.
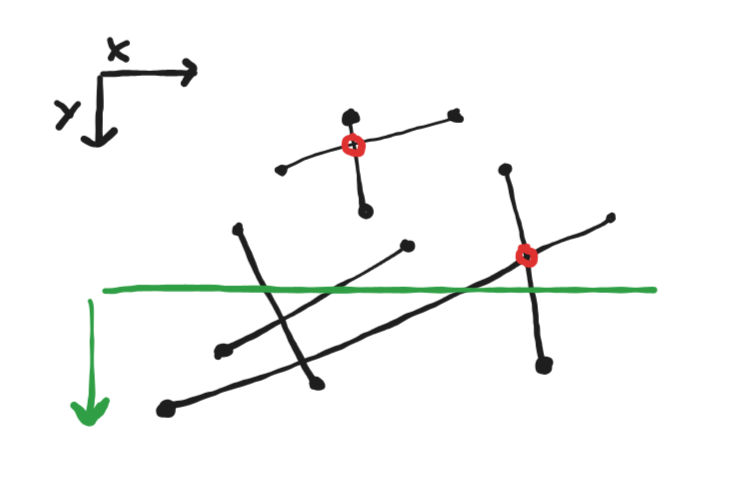
This method combined with the right data structures can speed up some calculations dramatically. The strategy is not limited to lines, but can be extended to planes and higher dimensions in general.
