Repeated Dijkstra

Introduction

When calculating if a railway connects to the end of the map for Train Apokalypse (see Projects), we ran into some trouble: The network is very large and the pathfinding algorithm that was used took about ~2ms for each call. This overview describes how to improve performance by using a very simple and dynamic method. It is written for readers that already knows a little bit about graphs and pathfinding algorithms.

What we initially had, was just the normal Dijkstra Algorithm (Wikipedia: Dijkstra) implemented with a Priority Queue (which used a Binary Heap as its underlying structure). We then repeatedly called this method when we wanted to know if there is still a path to the target (the end of the map) whenever we placed down a tile when generating the world.
Now of course, the first thing one could do, is to either improve the performance of the existing algorithm, by changing the data structure or optimizing it (for example by using Unitys Job System). Another option is to find a good heuristic and use A* (Wikipedia: A*).

Third Option

But there is another alternative, that can be used especially for this situation, because

1. We don’t care about the optimal path (any path will do)
2. We ask the algorithm the same question each time, because we just want to know if it is possible to reach a very specific Target Vertex in a graph.

So for those reasons, it is possible to reuse the results of previous calls for the next calls!

The idea is summarized very quickly:

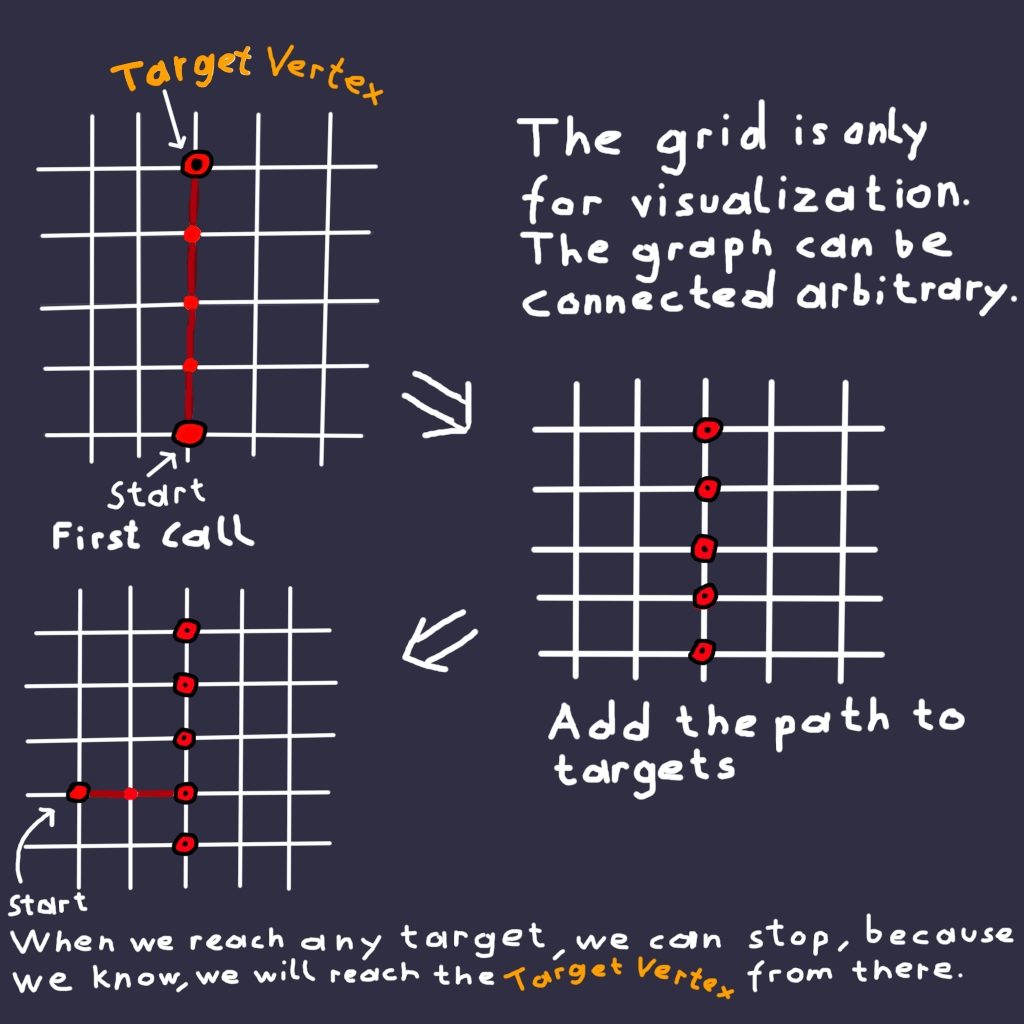
1. Use Dijkstra as usual and find a path to the Target Vertex.
2. Save that path into a list. Optionally you can use a dictionary or map and use the index of the Target Vertex as a hash for the path.
3. The next time you search for a path using Dijkstra (from a different position) you simply add the vertices of the previous path to the list of targets to search for.

Why is this faster? Because now the algorithm does not only stop when it reaches the target, but also when it reaches a vertex of the previous path! And that behaviour is correct, because we already know that it leads to the Target Vertex from the first call!

A Picture Says More

Problems

So, about the caveats. There is one thing that is a little bit problematic, and that is updating the network. It is not a problem as long as you are not removing anyhing from the paths you stored for this dynamic approach.
But if you do remove a verex or an edge on a path, there are a few things you can do (that we could think of).

• The first option is to just throw away the path. If your network is large, and not that well connected, this just means that you are a little bit inefficient, but it shouldn’t be a problem as long as the number of paths you hit when removing something is small.
• The second option is to cut the path into two pieces (assuming you saved the order). So you would keep everything after the removed vertex and throw away everything before. This is more efficient, because you keep more targets, but adds a little bit of complexity.

Conclusion

Here are the Unity profiler results.